[22’ ICLR] LoRA: Low-Rank Adaptation of Large Language Models
카테고리: Language
🔍 Abstract
 (출처: LoRA and DoRA from Scratch)
(출처: LoRA and DoRA from Scratch)
거대한 LLM을 downstream task를 위해 full fine-tuning을 진행하는 것은 경제적이지 못하다. 지금까지 adapter, prompt tuning 등 다양한 PEFT(Parameter-Efficient Fine-Tuning) 방법론이 제안되었지만, 이 논문에서는 이들의 단점을 지적하며 low-rank adaptation이라는 방법을 통해 이를 모두 해결할 수 있다고 한다. 이 논문은 ICLR 2022에 제출되었으며, LoRA라는 이름으로 발표되었다. LoRA는 지금까지도 굉장히 많은 수의 LLM fine-tuning에 사용되는 핵심적인 방법이기 때문에, 이 논문을 분석하며 깊이 있게 이해해보고자 한다.
1. Introduction
기존 연구 (Aghajanyan et al. (2020))에서 밝혀진 바에 따르면 pre-trained LM은 very low intrinsic dimension을 가지고 있다. 즉, 전체 parameter를 fine-tuning 하는 데에 어떠한 low dimension reparametrization이 가능하다는 것이다. 아래 그림과 같이, pre-training이 지속됨에 따라 실제 모델의 parameter는 low dimension manifold에 위치하게 된다.
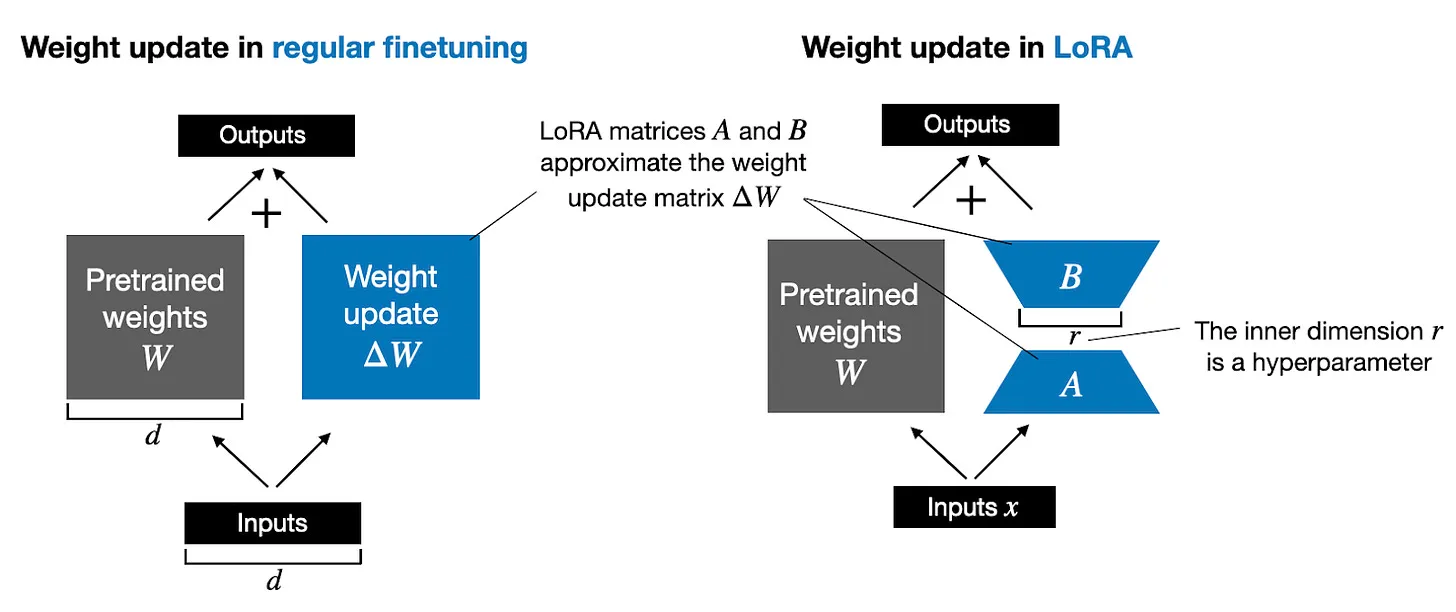
LoRA는 이러한 점을 이용하여 LLM의 low-rank reparametrization을 제안한다. Concept은 아래 그림과 같다.
2. Aren’t Existing Solutions Good Enough?
일반적인 LLM fine-tuning 방법은 LLM의 pre-trained weights $\Phi_ 0$로부터 시작하여 최종적으로 $\Phi_ 0 + \Delta \Phi$를 얻는 것이라고 볼 수 있다. 그러나, 이러한 방법은 $\Delta \Phi$의 dimension이 $\Phi$와 같다. GPT-3의 경우 175B parameter를 가지고 있으므로, 이는 굉장히 큰 dimension이고, 따라서 학습에 어려움이 따른다. 대신 LoRA는 $\Delta \Phi = \Delta \Phi (\Theta)$로 표현하며, 이때 $\Theta$는 smaller-size parameter이다. 이러한 방법은 compute-efficient하며 memory-efficient하다. 그러나 이러한 방법은 이미 위에서 제안한 여러 방법론들, 즉 Adapter Tuning, Prefix Tuning, Prompt Tuning과 같은 방법들과 동일한 방향성을 가지고 있다. 따라서 논문에서는 이러한 방법들과의 비교를 통해 LoRA의 효과를 입증하는 과정도 포함되어 있다. 결론만 정리하자면 다음과 같다.
- Adapter Tuning(Adapter): Adapter는 serial layer로 적용되기 때문에 inference latency가 생긴다. LoRA는 이러한 latency를 추가로 가지지 않는다.
- Prefix Tuning(PrefixLayer), Prompt Tuning(PrefixEmbed): 이러한 방법들은 최적화가 어렵다. 또한, sequence length를 추가로 차지하기 때문에 downstream task에 필요한 sequence length를 차지하게 된다. LoRA는 이러한 단점을 가지지 않는다.
3. Low-Rank Adaptation
그렇다면 LoRA의 방법을 조금 더 자세히 알아보자. 저자들은 pre-trained LM이 low intrinsic dimension을 가지고 있다는 것으로부터 adaptation (혹은 fine-tuning) 과정의 weight update도 일종의 low intrinsic rank를 가지고 일어날 것이라고 가정한다. 기존의 pre-trained LM layer의 weight를 $W_0 \in \mathbb{R}^ {d \times k}$라 하고, 이 layer에서 fine-tuning을 통해 얻게 될 weight를 $W_0 + \Delta W$라 하자. 위 가정에 의해, 다음과 같이 low-rank decomposition이 가능하다.
\[W_ 0 + \Delta W = W_ 0 + BA, \quad \text{where } B \in \mathbb{R}^ {d \times r}, A \in \mathbb{R}^ {r \times k}\]이때 rank $r$은 $r \ll \min(d, k)$이다. 구현 시에는 $A$는 Gaussian Initialization, $B=0$으로 초기화하여 첫 학습 때에는 기존과 동일하게 $\Delta W = 0$이도록 하였다. Inference 시에는 $W = W_ 0 + BA$로 계산해두고 사용하면 되기에, 추가적인 inference latency가 생기지 않는다.
실제로 저자들이 Transformer에 이를 적용할 때에는 Attention Module에만 적용하였고, MLP Layer에는 적용하지 않았다. 이러한 방식으로 VRAM 사용량을 거의 1/3으로 줄일 수 있었고, Checkpoint의 경우 1/10000 크기로 줄일 수 있었다.
다른 모델들, 즉 Adapter Tuning (Adapter), Prefix Tuning (PrefixLayer), Prompt Tuning (PrefixEmbed)와 비교했을 때에도 LoRA가 성능이 우수했다.
4. Understanding the Low-Rank Updates
4.1. Optimization Lessons
저자들은 추가로 LoRA에 대한 분석을 수행하여 LoRA가 어떻게 작동하는지, 성능을 높이기 위해서는 어떻게 해야 하는지를 알려준다. 이를 정리해보면 다음과 같다.
- Optimization Lesson 1. Larger rank로 적은 수의 weight을 LoRA로 학습시키는 것보다 작은 rank로 많은 수의 weight을 학습시키는 것이 더 효과적이다.
- Optimization Lesson 2. Rank가 작아도 충분히 좋은 성능을 낸다. 이는 실제로 update matrix $\Delta W$가 small instrinsic rank를 가지고 있다는 것을 보여준다.
이를 더 직접적으로 증명하기 위해 저자들은 $r=8$과 $r=64$에 대해 각각 adaptation matrix $A_ {r=8}$, $A_ {r=64}$를 SVD로 분해한 뒤, right-singular unitary matrix $U_ {r=8}$, $U_ {r=64}$의 유사도를 계산하였다. 이는 결국 subspace similarity를 계산한 것인데, 시각화한 결과는 아래와 같다.
그림을 보면, 각각의 top singular vector는 유사도가 높지만, 다른 singular vector들은 유사도가 낮다. 즉, top singular vector direction은 $r=8$이나 $r=64$에서 모두 중요한 역할을 하지만, 나머지 direction은 대부분 training 도중에 축적된 random noise의 비율이 높을 것이라고 추측할 수 있다. 별로 중요하지 않기 때문에 유사도가 높지 않다는 것이다. 이로부터 다시 한 번 adaptation matrix의 low-rank property를 확인할 수 있고, $r=1$인 경우에도 성능이 크게 떨어지지 않는 이유를 설명할 수 있다.
한편 동일한 방법으로 $r=64$인 random seed 모델 2개에 대해 subspace similarity를 계산한 결과는 다음과 같다.
$W_ q$의 경우 유사도가 높은 singular vector의 수가 많지만, $W_ v$의 경우 유사도가 높은 singular vector의 수가 적다. 이는 Optimization Lesson 3을 시사한다.
- Optimization Lesson 3. $W_ q$ (Query Matrix)의 intrinsic rank가 $W_ v$ (Value Matrix)의 intrinsic rank보다 더 높다. 따라서 사용할 수 있는 계산량이 제한적인 상황에서 $W_ q$에 대해 더 큰 rank를 사용하는 것이 더 효과적일 수 있다. (이는 Self-Attention에 대한 직관과 잘 맞아떨어진다. Value는 그 값을 거의 그대로 사용해도 되는 반면 Query는 말 그대로 Query의 역할을 하기 위해 더 많은 변환을 거쳐야 하기 때문이다.)
4.2. $W$ vs. $\Delta W$
마지막으로 저자들은 $W$와 $\Delta W$를 서로 비교하여 다음과 같은 결론을 얻었다. 수학적인 내용은 약간 생략하였다.
- $W$ vs. $\Delta W$.
- $W$와 $\Delta W$는 유사한 부분이 있다. 즉, 이미 $W$에 있는 feature 일부를 $\Delta W$가 재학습하여 강화하는 역할을 한다.
- 이때, $\Delta W$는 W의 top singular direction이 아니라 다른 direction, 즉 $W$에서는 중요하다고 생각되지 않는 direction을 강조한다. 위 그림을 보면, $W$에서 우선순위가 낮은 singular vector와의 유사도가 높은 것을 확인할 수 있다. 이때 그 강조의 정도는 굉장히 크다.
- 즉, LoRA는 pre-training model에서 이미 학습되었지만 강조되지 않았던, downstream task에서 중요한 feature를 다시 강조하는 역할을 한다고 볼 수 있다.
💡 Summary
지금까지 중요한 PEFT 방법인 LoRA를 알아보았다. LoRA는 fine-tuning matrix의 low-rank property를 이용하여 low-rank decomposition을 수행하는 방법으로 요약할 수 있다. LoRA는 Adapter Tuning과 달리 inference latency가 없으며, Prefix Tuning과 Prompt Tuning보다 최적화가 쉽기에 지금까지도 많이 사용되고 있다.
또한 Optimization Lesson을 통해 최대한 많은 수의 weight을 학습시키는 것이 더 효과적이며, $W$와 $\Delta W$의 비교를 통해 LoRA가 pre-training model에서 중요하다고 생각되지 않았던 feature를 강조하는 역할을 한다는 것을 알 수 있었다.
댓글 남기기