[CS236n] 9. Score Based Models (2)
카테고리: CS236n
태그: Diffusion Generation
💡 이 글은 『2024 YAI 봄전반기 생성모델팀』으로 진행되었으며, CS236n Fall 2023를 따라 정리했습니다.
1. Noise Conditional Score Networks (NCSN)
[CS236n] 8. Score Based Models (1)에서 Langevin dynamics를 사용하여 sampling을 수행하는 방법이 실제로 작동하지 않음을 확인하였다. 이번 장에서는 이를 해결하기 위한 방법으로 Noise Conditional Score Networks (NCSN)을 소개한다.
1.1. Annealed Langevin Dynamics
NCSN의 아이디어는 Gaussian perturbation을 사용하여 sampling을 수행하는 것이다. 즉, data distribution이 일부 공간에만 집중되어 있어 나머지 공간에서 score function의 계산이 불가능하므로, 이 공간을 Gaussian perturbation을 통해 넓혀 주는 것이다.
즉, 원래는 다음과 같이 data density가 일부 공간에만 집중되어 있어 나머지 공간에서는 score function estimation이 부정확했는데,
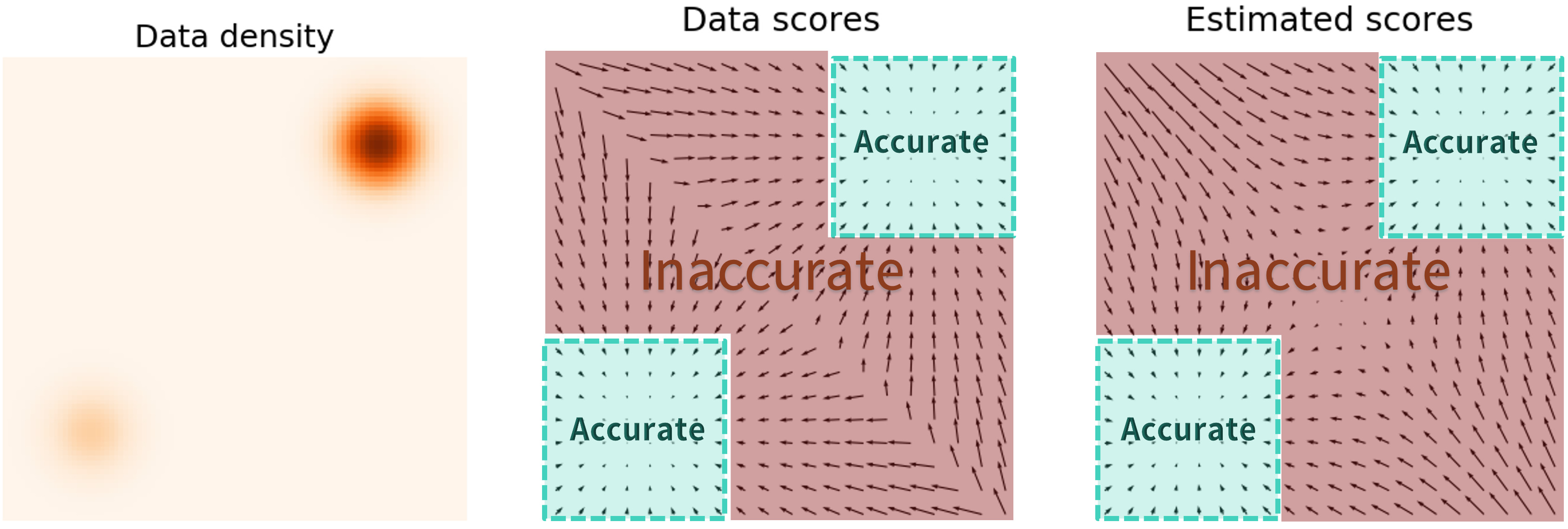
Gaussian perturbation을 통해 다음과 같이 data density가 넓어지게 되면 score function estimation이 가능해진다.

이러한 방법으로 Langevin dynamics의 문제는 해결했지만, 이제 또 다른 문제가 발생한다. Perturbed density는 더 이상 true data density가 아니라는 것이다. 이를 해결하기 위해 multi-scale noise perturbation을 사용한다. 즉, 시간이 지날수록 noise의 크기를 줄여 true data density에 가깝게 만드는 것이다.
이를 반복하면 다음과 같이 multi-scale noise perturbation을 통해 true data density에 가까워지게 된다. (여기서는 3개의 scale을 사용하였고, $\sigma_3 > \sigma_2 > \sigma_1$ 순으로 이동한다. 위 Figure에서 사용한 넘버링과 정반대이므로 주의.)
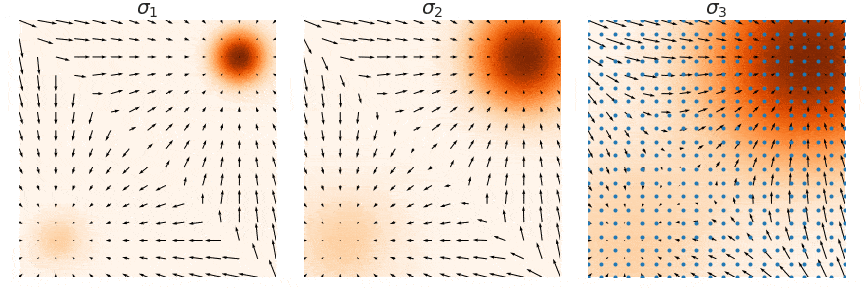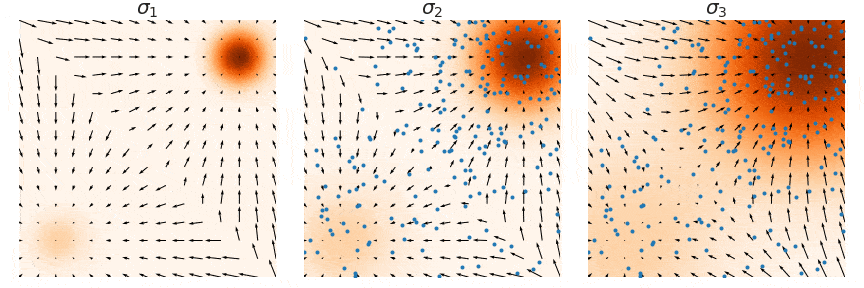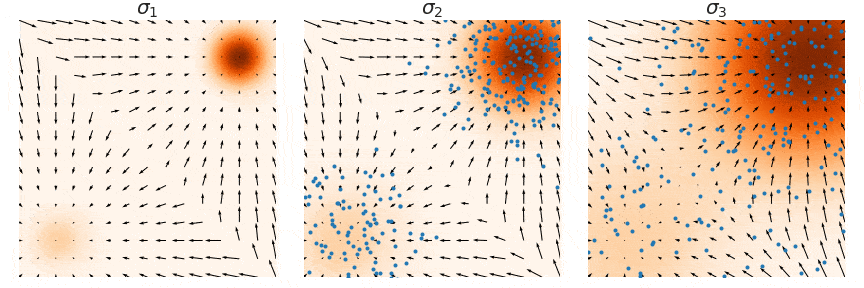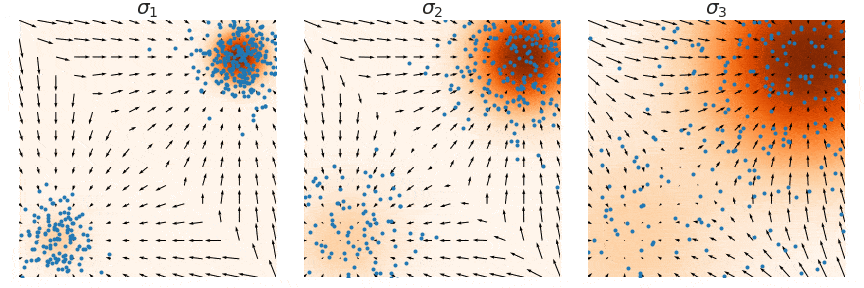
이 방법을 사용하면 Langevin dynamics의 두 번째 문제였던 data mode mixing 문제도 아래와 같이 해결된다.
이것이 Annealed Langevin Dynamics이다. 실제 알고리즘을 보면 $\alpha_i$를 조절하며 noise를 줄여나가는 것을 확인할 수 있다.
1.2. Noise Conditional Score Networks
이와 같은 방법을 사용하면 score function은 data $x$의 함수일 뿐만 아니라 noise $\sigma$의 함수이기도 하다. 따라서 이러한 score function을 모델링한 것이 Noise Conditional Score Networks (NCSN)이다. 이제 notation을 $s_\theta(x)$가 아닌 $s_\theta(x, \sigma)$로 바꾸어야 한다.
그렇다면 NCSN을 학습하기 위해 어떤 score matching loss를 사용할 것인가? Denoising score matching, sliced score matching 모두 가능하지만 denoising score matching의 경우 원래 목표가 perturbed data distribution의 score를 예측하는 것이므로, 현재 목표와 더 비슷하다. 따라서 일반적으로 denoising score matching을 사용한다. Denoising score matching loss에 각 $\sigma$의 weight $\lambda(\sigma)$를 곱하여 다음과 같이 나타낼 수 있다. 3번째 식은 $\tilde{x} = x + \sigma_i z$로부터 얻은 것이다.
\[\begin{aligned} & \frac{1}{L} \sum_{i=1} ^L \lambda(\sigma_i) \mathbb{E}_ {q_{\sigma_i}(x)} \left[ \left\Vert \nabla_x \log q_{\sigma_i}(x) - s_\theta(x, \sigma_i) \right\Vert_2^2 \right] \\ =& \frac{1}{L} \sum_{i=1} ^L \lambda(\sigma_i) \mathbb{E}_ {x \sim p_{data}, z \sim \mathcal{N}(0, I)} \left[ \left\Vert \nabla_{\tilde{x}} \log q_{\sigma_i}(\tilde{x} \vert x) - s_\theta(\tilde{x}, \sigma_i) \right\Vert_2^2 \right] + \text{const.} \\ =& \frac{1}{L} \sum_{i=1} ^L \lambda(\sigma_i) \mathbb{E}_ {x \sim p_{data}, z \sim \mathcal{N}(0, I)} \left[ \left\Vert s_\theta (x + \sigma_i z, \sigma_i) + \frac{z}{\sigma_i} \right\Vert_2^2 \right] + \text{const.} \\ \end{aligned}\]1.3. Setting
그럼 이제 몇 가지 변수들을 결정해야 한다. 첫 번째는 $\sigma_1$, 즉 maximum noise의 크기를 어떻게 정할 것인가에 대해 논의해야 한다. 일반적으로 $\sigma_1$은 datapoint 간 pairwise distance 중 최댓값 정도로 설정한다. 그 이유는, 처음에 샘플링한 데이터가 적어도 다른 data distribution으로 옮겨갈 수는 있게 하기 위함이다.
그리고 $\sigma_1$부터 $\sigma_L$까지 어떻게 감소할지를 정해야 한다. 일반적으로는 다음과 같이 정한다.
\[\frac{\sigma_1}{\sigma_2} = \frac{\sigma_2}{\sigma_3} = \cdots = \frac{\sigma_{L-1}}{\sigma_L}\]그리고 각 $\sigma$에 대한 loss의 비율, weight function $\lambda(\sigma)$도 결정해야 한다. $\sigma_i$가 증가할수록 예측이 어렵기에, $\lambda(\sigma)$도 이에 따라 증가하는 함수로 정한다. 일반적으로 $\lambda(\sigma_i) = \sigma_i^2$로 설정한다. 이때 loss function은 다음과 같이 정리된다.
\[\begin{aligned} & \frac{1}{L} \sum_{i=1} ^L \sigma_i^2 \mathbb{E}_ {x \sim p_{data}, z \sim \mathcal{N}(0, I)} \left[ \left\Vert s_\theta (x + \sigma_i z, \sigma_i) + \frac{z}{\sigma_i} \right\Vert_2^2 \right ] \\ =& \frac{1}{L} \sum_{i=1} ^L \mathbb{E}_ {x \sim p_{data}, z \sim \mathcal{N}(0, I)} \left[ \left\Vert \sigma_i s_\theta (x + \sigma_i z, \sigma_i) + z \right\Vert_2^2 \right] \\ \end{aligned}\]그리고 여기서 noise $\epsilon_\theta (\cdot, \sigma_i) := \sigma_i s_\theta (\cdot, \sigma_i)$로 정의하면, loss function은 다음과 같이 정리된다.
\[\frac{1}{L} \sum_{i=1} ^L \mathbb{E}_ {x \sim p_{data}, z \sim \mathcal{N}(0, I)} \left[ \left\Vert \epsilon_\theta (x + \sigma_i z, \sigma_i) + z \right\Vert_2^2 \right]\]1.4. Sampling
실제 샘플링 과정은 다음과 같이 정리할 수 있다.
- Datapoints $\lbrace x_1, x_2, \cdots, x_n \rbrace \sim p_{data}$를 샘플링한다.
- Noise scale indices $\lbrace i_1, i_2, \cdots, i_n \rbrace \sim \text{Uniform}(1, L)$를 샘플링한다.
- Gaussian noise $\lbrace z_1, z_2, \cdots, z_n \rbrace \sim \mathcal{N}(0, I)$를 샘플링한다.
- 다음과 같이 score matching loss를 추정한다.
이를 통해 CIFAR-10 data generation을 수행한 모습이다.

이를 통해 high quality image generation도 가능하다.

2. SDE (Stochastic Differential Equation)
2.1. Stochastic process
지금까지의 과정은 큰 noise $\sigma_1$에서 시작하여 작은 noise $\sigma_L$로 이동하면서 true data distribution에 가까워지는 과정이었다.
이 과정을 연속적으로 표현하면 다음과 같다.
즉, $p_T(x) \approx \pi(x)$로부터 시작하여 $p_t(x)$를 거쳐 $p_0(x) = p_{data}(x)$로 이동하는 것이다. 반대로, $p_0(x) = p_{data}(x)$로부터 시작하여 $p_t(x)$를 거쳐 $p_T(x) \approx \pi(x)$로 이동하는 것도 가능하다. 이러한 과정을 stochastic process라고 하고, 이를 통해 data의 perturbation이 가능하다.
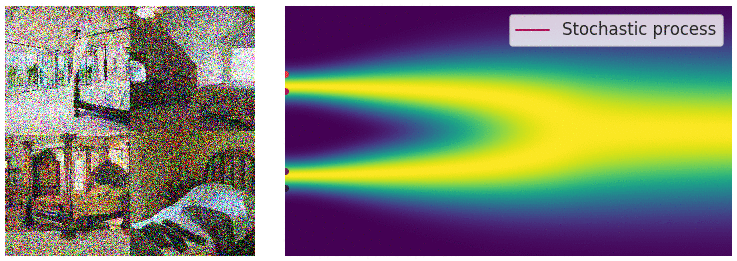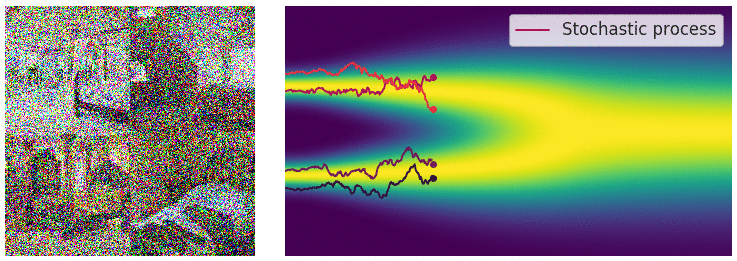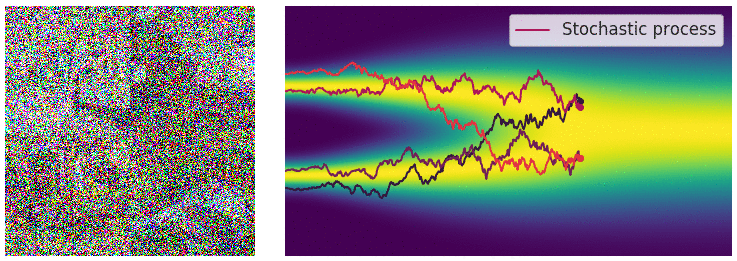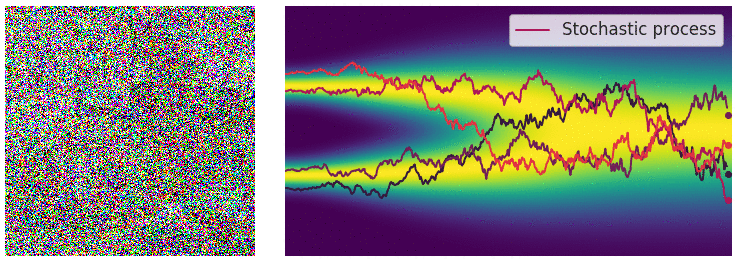
이 과정을 stochastic differential equation (SDE)로 표현하면 다음과 같다.
\[dx_t = f(x_t, t) dt + g(t) dw_t\]이때 $f(\cdot, t)$는 drift coefficient, $g(t)$는 diffusion coefficient라고 불린다. Drift coefficient는 deterministic한 과정을 나타내며, noise에 의해 평균적으로 이동하는 방향을 나타낸다. Diffusion coefficient는 stochastic한 과정을 나타내며, noise의 크기를 나타낸다. 여기서 $w$는 standard Brownian motion이고, 따라서 $dw$는 infinitesimal white noise로 생각할 수 있다.
이러한 stochastic process에는 해당하는 reverse stochastic process가 대응된다. 우리가 원하는 것은 noise로부터 원래 data distribution으로 이동하는 것이므로, 우리가 원하는 것은 reverse stochastic process이다.
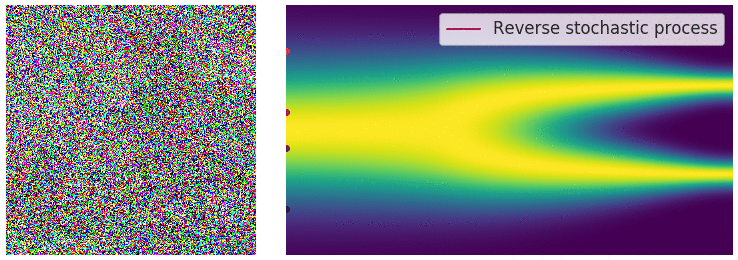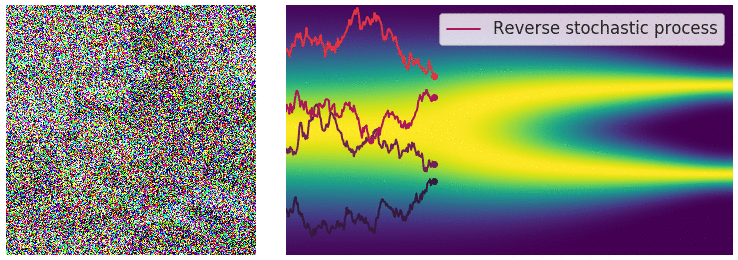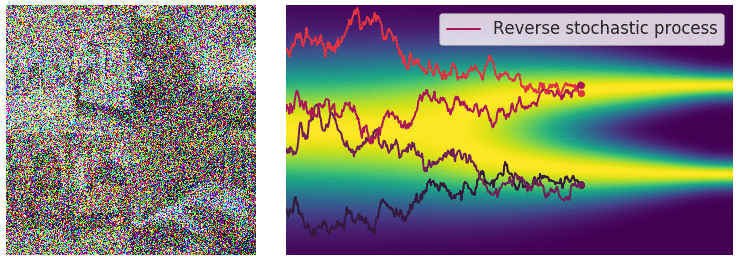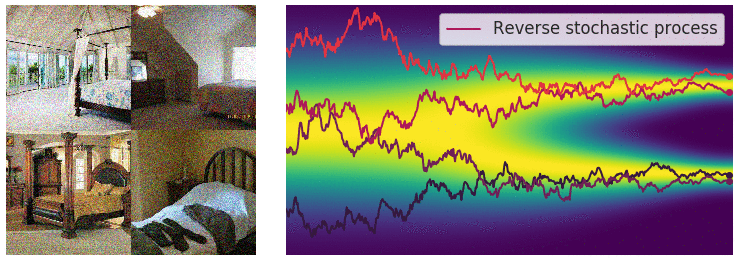
이때 reverse SDE는 다음과 같이 구할 수 있다. 아래 식을 통해, Reverse SDE를 풀기 위해서는 score function $\nabla_x \log p_t(x)$를 구해야 한다는 것을 알 수 있다.
\[dx_t = \left[f(x,t) - g^2 (t) \nabla_x \log p_t(x) \right] dt + g(t) d \bar{w}_ t\]

Stochastic process의 $f$와 $g$는 우리가 설정할 수 있는데, 여기서는 간단하게 다음과 같이 SDE 및 reverse SDE를 설정한다.
\[\begin{aligned} dx_t &= \sigma (t) dw_t \\ dx_t &= - \sigma (t) ^2 \nabla_x \log p_t(x_t) dt + \sigma (t) d \bar{w}_ t \end{aligned}\]지금까지의 내용을 수식으로 정리하면 다음과 같다. 여기서는 Euler-Maruyama method를 사용하여 SDE를 풀었다. 그리고 reverse SDE이므로, $\Delta t \lt 0$이다.
- Time-dependent score-based model: $s_\theta(x, t) \approx \nabla_x \log p_t(x)$
- Training: $\mathbb{E}_ {t \sim \mathcal{U} (0, T)} \left[ \mathbb{E}_ {p_t(x)} \left[ \left\Vert \nabla_x \log p_t(x) - s_\theta(x, t) \right\Vert_2^2 \right] \right]$
- Reverse-time SDE: $dx_t = - \sigma (t) ^2 s_\theta (x,t) dt + \sigma (t) d \bar{w}_ t$
- Euler-Maruyama: $x_{t+\Delta t} = x_t - \sigma (t) ^2 s_\theta (x,t) \Delta t + \sigma (t) z$, where $z \sim \mathcal{N}(0, \vert \Delta t \vert I)$
2.2. Predictor-corrector sampling method
Predictor-corrector sampling method는 이것을 더 발전시킨 방법으로, numerical SDE solver를 사용하여 얻은 trajectory를 MCMC를 사용하여 fine-tuning 하는 것이라고 생각하면 된다. 여기서 numerical SDE solver는 predictor, score-based MCMC는 corrector에 해당한다.
즉, Euler-Maruyama method와 같은 numerical SDE solver를 사용하여 $x_t \sim p_t(x)$로부터 $x_{t+\Delta t} \sim p_{t+\Delta t}(x)$를 얻은 후, 이를 Langevin MCMC와 같은 MCMC method를 사용하여 fine-tuning하여 $p_{t+\Delta t}(x)$로부터 higher-quality sample을 얻는 것이다.
이를 활용하면 다음과 같이 1024x1024 이미지에 대해서도 high-quality image generation이 가능하다.

2.3. Probability flow ODE
지금까지 한 가지 문제가 남아있다면 log-likelihood를 계산할 수 없다는 것이다. 따라서, 이를 해결하기 위해 probability flow ODE를 사용할 수 있다. 간단하게 설명하자면 SDE를 푸는 것이나 ODE를 푸는 것이나 별반 다르지 않은데, ODE를 사용하면 샘플링이 간편하고 log-likelihood를 계산할 수 있다는 장점이 있다. Reverse SDE에 대응하는 ODE는 다음과 같이 쓸 수 있다.
\[\frac{dx_t}{dt} = - \frac {1}{2} \sigma (t) ^2 \nabla_x \log p_t(x_t)\]이때 $\nabla_x \log p_t(x_t) \approx s_\theta(x_t, t)$를 사용한다. SDE와 동일한 marginal distribution $p_t(x)$를 가지면서 다음과 같이 ODE를 풀 수 있는 것이다.
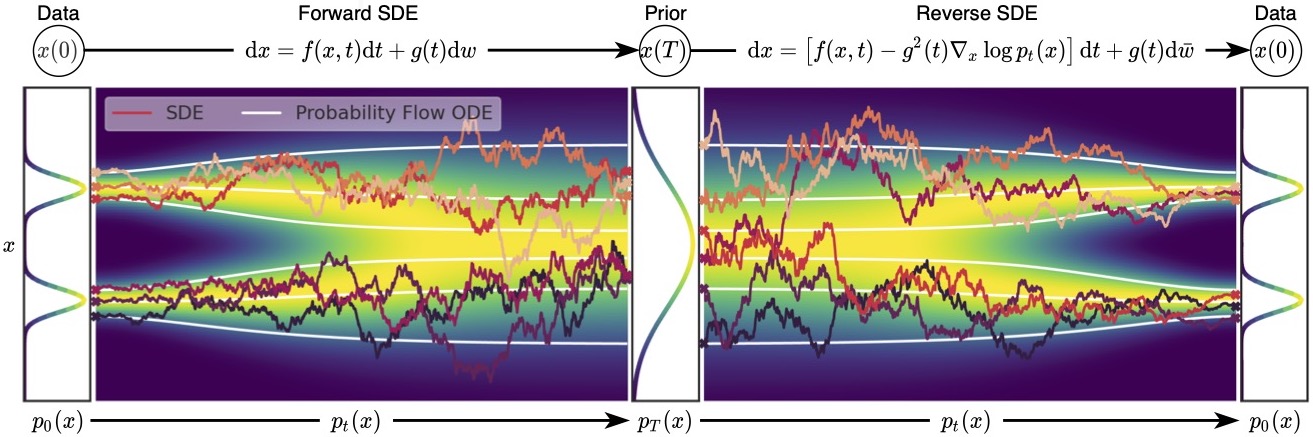
Change of variables formula를 통해 다음 식을 유도할 수 있다. 이는 noise distribution $p_T(x)= \pi(x)$로부터 data distribution $p_0(x) = p_\theta(x)$를 추정한다는 점에서 normalizing flow model으로 볼 수도 있다. 이러한 모델은 다양한 부분에서 SOTA를 달성했다.
\[\log p_\theta(x_0) = \log \pi(x_T) - \frac {1}{2} \int_0 ^T \sigma (t) ^2 tr (\nabla_x s_\theta(x, t)) dt\]3. Controllable Generation Process
Score-based model은 controllable generation process를 구성하기에 적합하다. 먼저 $p(x)$의 분포를 잘 알고 있고, forward process를 통해 $p(y \vert x)$를 구할 수 있다고 가정하자. 예를 들어 동물 데이터의 분포 $p(x)$가 있고, 동물의 label을 예측하는 classifier $p(y \vert x)$가 있다고 하자. 우리는 label $y$를 주고, 그에 해당하는 동물 이미지를 생성하고 싶다. 즉, posterior(inverse distribution) $p(x \vert y)$를 구하고 싶다.
원래 posterior는 다음과 같이 나타낼 수 있고, $p(y)$를 구할 수 없다는 문제가 있다.
\[p(x \vert y) = \frac{p(x) p(y \vert x) }{p(y)}\]그러나 posterior의 score function은 다음과 같다.
\[\nabla_x \log p(x \vert y) = \nabla_x \log p(x) + \nabla_x \log p(y \vert x) - \nabla_x \log p(y)\]그런데 $\nabla_x \log p(y) = 0$이므로, $p(y)$를 구할 필요가 없어졌다. 따라서 posterior의 score function을 사용하여 controllable generation process를 구성할 수 있다. 이때 $\nabla_x \log p(x)$는 unconditional score, 즉 일반적인 데이터셋에서 score-based model이 예측할 수 있는 값이고, $\nabla_x \log p(y \vert x)$는 이미 알고 있는 forward model에서 계산할 수 있는 값이다. 여기서 우리는 forward model만 바꾸면서, 동일한 score-based model을 사용하여 여러 process를 구상할 수 있다.
예를 들어 stroke painting으로부터 image를 생성하는 task를 수행할 수 있다. 이때 forward model, 즉 image로부터 stroke painting을 생성하는 model을 만드는 것은 그렇게 어렵지 않을 것이다. 그리고 이미지에 대해 score-based model을 학습하면, 결과적으로 이 둘을 통해 stroke painting으로부터 image를 생성할 수 있다.
Captioning model을 forward model으로 가지고 있다면 다음과 같은 language-guided image generation task도 수행할 수 있다.
4. Summary
Score-based model은 많은 장점을 가지고 있다.
- Gradients of distributions (scores) 의 추정이 쉽다.
- Normalizing, invertible condition 등이 필요하지 않아 model architecture가 자유롭다.
- GAN에서의 minimax와 같은 최적화 과정이 없어 학습이 안정적이다.
- GAN과 비교하여 비슷하거나 더 좋은 sample quality를 보여준다.
- Likelihood 계산이 가능하다.
앞 과정에 이어 [CS236n] 9. Score Based Models (2)에서는 Score-based model에서 Langevin dynamics를 사용하여 sampling을 수행하는 것은 실제로 작동하지 않음을 확인하였다. 이를 해결하기 위해 Noise Conditional Score Networks (NCSN)을 소개하였다. 이는 Annealed Langevin Dynamics을 사용하여 sampling을 수행하는 방법이다. 그리고 SDE (Stochastic Differential Equation)를 통해 이를 일반화할 수 있었으며, predictor-corrector sampling method 및 probability flow ODE를 통해 이를 발전시켰다. 마지막으로 controllable generation process를 구성하는 방법에 대해 이야기했다.
댓글 남기기