[CS236n] 2. Autoregressive Models

Date: 2024.03.08 Updated: 2024.03.08

카테고리: CS236n

💡 이 글은 『2024 YAI 봄전반기 생성모델팀』으로 진행되었으며, CS236n Fall 2023를 따라 정리했습니다.

1. Autoregressive model

1.1. Introduction

1장으로부터, 생성모델에서 중요한 부분은 1) 어떻게 데이터의 분포 $p(x)$를 잘 표현하는 모델 $\mathcal{M}$을 만들 것인지, 그리고 2) 그것을 어떻게 학습할 것인지였다. 여기서는 그 모델의 가장 간단한 예시로 자가회귀모형(autoregressive model)을 소개한다. 3장에서는 어떻게 학습할 것인지의 예시로 최대우도학습(maximum likelihood learning)을 소개할 것이다.

Autoregressive model은 일종의 시계열 모델로, $i$번째 데이터 $x_i$가 그 이전의 데이터 $\mathbf x_ {\lt i}$, 즉 $x_1, x_2, \ldots , x_{i-1}$에만 영향을 받는다고 가정한다. 즉, chain rule에 의해 $p(\mathbf{x})=p(x_1, \ldots, x_n)$을 다음과 같이 표현할 수 있다.

\[p(\mathbf{x})=\prod_{i=1}^n p(x_i\mid x_1, x_2, \ldots, x_{i-1}) = \prod_{i=1}^n p(x_i\mid \mathbf{x}_ {\lt i})\]

만일 각각의 $x_i$가 0 또는 1만을 나타낼 수 있다면 $p(x_i\mid \mathbf{x}_ {\lt i})$를 표현하기 위해 필요한 파라미터는 총 $2^{i-1}$개이다. 이는 $(x_1, \ldots, x_i)$의 순서쌍에 따라 $p(x_i\mid \mathbf{x}_ {\lt i})$의 값을 정해주어야 하기 때문이다. 예를 들어, $p(x_3\mid x_1, x_2)$라면 $(x_1, x_2)=(0,0), (1,0), (0,1), (1,1)$에 대해 $p(x_3\mid x_1, x_2)$의 값을 결정해주어야 하므로 4개의 파라미터가 필요하다. 따라서, $p(\mathbf{x})=\prod(x_i\mid \mathbf{x}_ {\lt i})$를 표현하기 위해 필요한 파라미터 수는 다음과 같다.

\[1+2+4+\ldots+2^{n-1}=2^n-1 \sim O(2^n)\]

시간복잡도가 지수함수를 따르므로, 많은 리소스가 요구된다. 따라서 chain rule만을 사용하여 만든 autoregressive model은 수학적으로는 추가적인 가정이 필요하지 않은 완벽한 모델일지는 몰라도, 조금만 데이터량이 많아지더라도 모델의 크기가 지나치게 커진다. 따라서 추가적인 가정이 필요한데, 여기서는 Bayesian network와 Parametric neural model을 소개한다.

1.2. Bayesian network

베이지안 네트워크에서는 조건부 독립(conditional independence)를 가정한다. (모든 베이지안 네트워크가 이를 가정하는 것이 아니다. 간단한 생성모델에서 그렇다는 것이다.) 이는 conditional probability table(CPT)로 표현되며, 다음과 같이 $x_i$를 예측하기 위해 직전 $x_{i-1}$만 고려한다는 것이다.

\[p_{\mathrm{CPT}}(\mathbf{x}) = \prod_{i=1}^n p(x_i\mid x_1, x_2, \ldots, x_{i-1}) \approx \prod_{i=1}^n p(x_i\mid x_{i-1})\]

베이지안 네트워크를 사용하면 기존에 $p(x_i \mid \mathbf{x}_ {\lt i})$를 표현하기 위해 필요했던 $2^{i-1}$개의 파라미터 대신 $p(x_i\mid x_{i-1})$를 표현하기 위해 2개의 파라미터만 필요하다. 따라서 파라미터 수를 $2^{i-1}$개에서 $2n-1$개로 줄일 수 있다.

1.3. Parametric neural models

심층 신경망 구조에서는 $p(x_i \mid \mathbf{x}_ {\lt i})$를 매개변수화한다. 여러 매개변수화 방법이 있지만 가장 간단한 logistic regression을 도입한다고 가정하면 다음과 같다.

\[p_{\mathrm{Neural}}(\mathbf{x})=\prod_{i=1}^n p_{\mathrm{Neural}}(x_i\mid x_1, x_2, \ldots, x_{i-1}; \alpha^i)\] \[p_{\mathrm{Neural}}(x_i \mid x_1, x_2, \ldots, x_{i-1}; \alpha^i) = \sigma(\alpha_0^i+\alpha_1^ix_1+\dots+\alpha_{i-1}^ix_{i-1})\]

$p_{\mathrm{Neural}}(x_i \mid x_1, x_2, \ldots, x_{i-1}; \alpha^i)$를 표현하기 위해서는 파라미터 $i$개 $\alpha_0^i, \dots, \alpha_{i-1}^i$가 필요하므로, 총 파라미터는 대략 $n^2/2$으로 나타낼 수 있다. 따라서 chain rule에 의한 모델보다는 파라미터 수를 많이 줄였고, Bayesian network보다는 성능이 향상되기를 기대할 수 있다.

2. Fully visible sigmoid belief network (FVSBN)

FVSBN에서는 위 아이디어를 그대로 사용한다. 예를 들어 MNIST 데이터셋에 대해 픽셀 $X_1$이 주어졌을 때, 순차적으로 $X_2, \ldots, X_{784}$를 예측하기 위해 $X_i \in [0,1]$이라 가정하고 다음과 같이 모델링한다. 샘플링을 진행할 때는 $\bar{x}_ 1$을 랜덤으로 뽑고, 순차적으로 $\mathbf{x}_ {\lt i}$의 값에 따라 $\bar{x}_ i$를 뽑는다. 파라미터 수는 아까와 동일하게 대략 $n^2/2$이다.

\[\hat{x}_ i= p(X_i=1 \mid \mathbf{x}_ {\lt i}; \alpha^i)=\sigma(\alpha_0^i+\sum_{j=1}^{i-1}\alpha_j^i x_j)\]

FVSBN을 활용하여 Caltech 101 Silhouettes 데이터셋을 훈련한 뒤 샘플링한 결과는 다음과 같다. (좌: 데이터셋, 우: 샘플링)

3. Neural autoregressive density estimation (NADE)

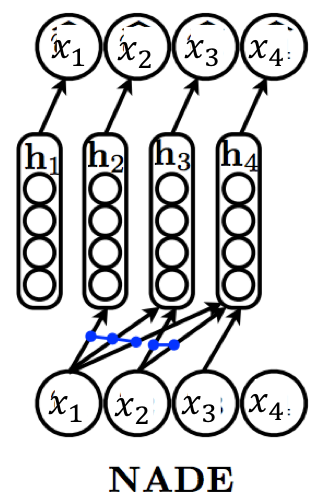
Neural autoregressive density estimation (NADE) 모델에서는 로지스틱 회귀 대신 hidden layer가 있는 심층 신경망을 사용한다. 심층 신경망 $h_i$의 weight, bias를 각각 $W_ {\lt i}, c_i$라고 하면 hidden layer의 식을 다음과 같이 쓸 수 있다.

\[h_i = \sigma(W_ {\lt i} \mathbf{x}_ {\lt i}+c_i)\]

그리고 최종 샘플링 $\bar{x}_ i$는 다음과 같이 쓸 수 있다.

\[\hat{x}_ i= \mathrm{softmax}(\alpha_ih_i+b_i)\]

이때 파라미터의 수는, 만약 $h_i \in \mathbb{R}^ d$라면 다음과 같다: $W_ {\lt i} \in \mathbb{R} ^{d \times i}, c_i \in \mathbb{R}^ d, \alpha_i, b_i \in \mathbb{R}^ {d+1}$. 따라서 $i=1, \dots, n$에 대해 모두 더하면 대략 $O(n^2d)$이다.

이를 줄이기 위하여, parameter sharing을 사용할 수 있다. 즉, 원래는 서로 다른 $W_ {\lt i}$에서 $x_i$를 hidden layer에 embedding하기 위해 모두 다른 weight $w_i$를 사용했다면, 이제는 서로 다른 $W_ {\lt i}$에서도 $w_i$를 공유하겠다는 것이다. 즉 다른 $h_i$에서도 $w_ix_i^T$ 성분은 동일하게 유지된다. 이를 활용하면 total weight $W \in \mathbb{R}^ {d \times n}$만 있으면 되므로, 대략 $O(nd)$로 파라미터를 줄일 수 있게 된다.

NADE을 활용하여 MNIST 데이터셋을 훈련한 뒤 샘플링한 결과는 다음과 같다. (좌: 데이터셋, 우: 샘플링)

4. Masked autoencoder for distribution estimation (MADE)

기존 autoencoder는 일반적인 생성모델과 달리 $\mathbf{x}_ {\lt i}$만 학습하는 것이 아니라 전체 $\mathbf{x}$를 활용하여 학습하도록 만들어졌으므로 생성모델이라고 할 수 없다. 그러나 $\mathbf{x}_ {\lt i}$만 활용하도록 mask를 사용한다면 생성모델로 사용할 수 있고, 이를 masked autoencoder for distribution estimation (MADE)라고 한다. 참고로 hidden layer에도 랜덤으로 숫자 $i$를 부여하여, $\mathbf{x}_ {\lt i}$에서 연결된 노드들만 연결하도록 하여 제한조건을 유지한다.

5. Application

5.1. NLP

자연어 처리(NLP)분야의 RNN(Recurrent Neural Network)도 autoregressive model의 일종이다. 기존 autoregressive model과 다른 점은 재귀적(recursive)으로 모델을 구성할 수 있다는 점이고, 그래서 입출력의 길이에 (이론상) 제한이 없다. 그러나 sequential evaluation, 즉 $x_1$을 입력하여 $x_2$를 받고, 다시 $x_2$를 넣어 $x_3$를 받는 일을 반복해야 하므로 오래 걸리고, step이 길어지면 exploding/vanishing gradients 문제가 발생한다는 문제가 있다.

이를 해결하기 위해 Attention based models, Generative transformers 등이 제안되었고, 이들 역시 autoregressive model 기반의 생성모델로 볼 수 있다.

5.2. Vision

Vision 계열의 autoregressive model로 PixelCNN (Oord et al. 2016)을 소개한다. 일반적인 CNN과는 달리 masked convolution을 사용하여 앞쪽 정보($\mathbf{x}_ {\lt i}$)만 활용할 수 있도록 하였다.

Imagenet(32 x 32)에 대한 훈련 결과는 다음과 같다.

5.3. Adversarial Attack

머신러닝 기법은 adversarial example에 취약하다. 간단한 noise를 더해주는 것으로만도 머신러닝 모델이 착각하게 만들 수 있다. 따라서 adversarial attack을 탐지하는 것이 중요하다.

Adversarial attack 분야에서의 autoregressive model의 예시로 PixelDefend (Song et al. 2018)를 소개한다. 컨셉은 다음과 같다.

clean input에 대해 생성모델 $p(x)$를 훈련시킨다.
새로운 input $\bar{x}$에 대하여 $p(\bar{x})$를 계산한다.
만약 adversarial example이라면, 일반적인 input에 비해 $p(\bar{x})$가 현저히 낮을 것이다.

6. Summary

[CS236n] 2. Autoregressive Models에서는 가장 간단한 생성 모델인 autoregressive model의 컨셉에 대해 알아보고, 그 예시로 FVSBN, NADE, MADE와 각 분야에서의 적용 예시로 RNN, PixelCNN, PixelDefend 등을 알아보았다. 다음 장에서는 이러한 모델을 “어떻게 훈련할지”에 대한 간단한 예시인 maximum likelihood learning에 대해 알아본다.

I'm rubatoyeong